- Research
- Open access
- Published:
Scoring and classifying regions via multimodal transportation networks
Applied Network Science volume 4, Article number: 97 (2019)
Abstract
In order to better understand the role of transportation convenience in location preferences, as well as to uncover transportation system patterns that span multiple modes of transportation, we analyze 500 locations in the Tokyo area using properties of their multimodal transportation networks. Multiple sets of measures are used to cluster regions by their transportation features and to classify them by their synergistic properties and dominant mode of transportation. We use twelve measures collected at five different radii for five distinct combinations of transportation networks to rank locations by their transportation characteristics. We introduce an additional 114 scores derived from the 300 measures to assess, among other things, access to public transportation, the effectiveness of each mode of transportation, and synergies among the modes of transportation. Additionally, we leverage those scores to classify our locations as being train-centric, bus-centric, or car-centric and to uncover geographic patterns in these characteristics. We find that business hubs, despite having low populations, are so conveniently reachable via train and road systems that they consistently achieve the highest sociability and convenience scores. Suburban regions have more serviceable bus systems, but lower connectivity overall resulting in lower reachable populations despite greater local populations. Even though Tokyo has the largest and densest public transportation system in the world we find that the road network consistently dominates the train and bus networks for all accessibility measures.
Introduction
Because transportation systems are so naturally seen as graphs/networks they are a common subject for graph theory and network analysis – including the original Königsberg bridge problem. Most studies of transportation networks focus on one mode: typically train (Derrible and Kennedy 2009; Derrible 2012), road (Crucitti et al. 2006), or air (Guimera et al. 2005) (for a review of how network theory has been applied to transportation systems see (Derrible and Kennedy 2011)) Although focusing on one mode allows for simpler analyses of structural patterns and similarities among cities, it is insufficient for characterizing how people use a transportation system. For example, one mode may compensate for another and/or using them together may be more effective than any single mode alone. The current work analyzes the transportation system of the Greater Tokyo Area (Tokyo, Kanagawa, Chiba, and Saitama prefectures) integrating the train, bus, and road systems along with a geographical hexagonal grid foundation. As such it includes highly urbanized areas, suburban areas, rural areas, desolate mountainous areas, and everything in between.
Although there exist purely graph theoretic studies of transportation networks in terms of measures like centrality scores, small world properties, etc., these kinds of networks are fundamentally geographically embedded. The physical constraints on the network structure requires the inclusion of continuous distance and time weights in otherwise discrete network measures. Furthermore, rather than focus on purely structural features, we perform an analysis that combines demographic data with geographically modified network methods. This is done at multiple time and distance scales in order to assess a variety of transportation and sociological characteristics such as transportation access limitations, synergies among distinct modes, transportation mode importance, and heterogeneity in transportation effectiveness.
For the purpose of utilizing machine learning techniques we perform an analysis of various transportation subnetworks centered on 500 randomly chosen locations within the Tokyo area. The individual transportation modes are combined in five different ways for each of five different distance/time thresholds and 12 networks measures are collected from each resulting subnetwork. We introduce an additional 114 scores derived from the 300 core measurements to assess higher-order features such as scaling patterns and mode synergies. We perform a battery of clustering experiments on selected network, spatial, and sociological measures in order to identify locations with similar characteristics and identify geographic patterns in those characteristics. In order to evaluate the appropriateness of different clustering techniques for different tasks we apply k-means, hierarchical, and spectral clustering and compare their results.
Data
Our analysis includes four separate transportation networks (train, bus, road, and hex) as well as walking links that connect the disparate networks together. In addition to these networks we utilize fine-grained population data distributed to each hex on the grid. The population and road network data are publicly available (as described below) while the train and bus networks come from proprietary third party data sources (Ekitan 2019).
Hexagonal geographic grid
The geographic foundation of our analysis is a 125m inner radius (54,127m2) hexagonal grid covering all of Japan. We use GoogleMap’s coordinates of Tokyo Station (139.7649361E, 35.6812405N) as a fixed reference point and grow the hexes outward from there. Because at different latitudes, the translation between meters and degrees changes, we use this method to ensure a true 250m hexagonal grid with minimal lat/lon distortion around Tokyo.
The 500 locations used in our clustering analysis are chosen from this hexagonal grid. They are also used as the sources and destinations of our network measures, hold the demographic data, form the basis for visualizing the data (as in Fig. 5), and act as the nodes for one of the transportation networks. We restrict the hex creation to within 1 km of the border/coastline of Tokyo, Kanagawa, Chiba, and Saitama prefectures using GIS shape data from (GADM 2018) excluding islands not reachable by train, bus, or road.
Demographic data
In order to assess practical (versus potential) accessibility we incorporate the population distribution into our analysis. We use 250m2 square grid population data obtained from (Official Statistics of Japan 2015) combined with mesh coordinates from (Association for Promotion of Infrastructure Geospatial Information Distribution 2015). However, instead of using the square grid as our locations, we interpolate the population of hexes Hi from square grid locations Sj using their overlap proportions as depicted in Fig. 1 using Eq. 1.
Demonstration of proportional resampling of square grid population data to our hex grid. The hex α has an interpolated population value calculated from its proportional overlap with the population data grid spaces A, B, C, and D. The population value for hex β is similarly constructed from the square grid spaces C, D, E, and F
This resampling method allows us to convert any geographical data into a common baseline with attractive geospatial properties; a feature which will be crucial for future work incorporating additional socioeconomic data. This resampling ability is especially important for Japan because most data is only available by administrative area (e.g. by city or some subdivision thereof), and even the available grid datasets utilize grids of differing resolutions and reference points.
Network data and construction
We utilize four separate networks representing distinct modes of transportation: rail, bus, road, and hex/local. The four transportation networks are connected to each other via walking links. All network edges in the current work are modeled as symmetric (undirected). Here we provide the details of each network and their integration.
Hex network
The hex network is created from the hexagonal grid by connecting each hex to its neighboring hexes. The generated links all have a length of 250 m and a traversal time of 3 min based on a 5 kph (walking) speed. This creates a transportation network representing slow local travel; usually walking, but may also represent driving on small streets to throughways, cycling, etc. As such, we use “walking links” to refer to the intermodal edges discussed below and “hex links” to refer to edges among hex nodes.
The hex network serves two main purposes. First, not all grid spaces are accessible directly via other transportation networks, so this ensures all hexes are reachable. Second, in many cases using purely transportation links based on the closest station/stop/intersection leads to unnatural and inaccurate travel times for locations. For example, for many suburban locations the closest station is one serviced by only local trains; however, there may be another station only slightly further away where an express/commuter train stops. The total travel time from such a location to the city center would therefore be shorter by walking to the station with an express train rather than using the closest station. Connecting the hexagonal grid spaces into a local transport network eliminates this problem while providing an intuitive shared geographic foundation for all the transportation networks.
Train network
Rail (train, subway, and streetcar) travel is considered the dominant mode of transportation in Japanese cities (Calimente 2012). The rail system in Tokyo is the densest in the world with the greatest ridership and frequency of trains (OECD Statistics 2016; Train Media 2017). Although in terms of sheer numbers of nodes and edges the bus and road networks are both larger than the train network (Table 1), for most urban areas the train network handles the greatest traffic in terms of the number of people per kilometer (Public Purpose 2003).
One natural and common representation of a rail network is to connect nodes representing each station with edges representing routes/tracks having stops at those stations (Barthélemy 2011). If distinct routes sharing tracks are captured as distinct edges, then this creates a multigraph (Goczyłla and Cielatkowski 1995). However, for our analysis the transfer times between trains/lines as well as platform waiting/exit times are crucial to the total travel times. In order to integrate these transfer and access times into our network algorithms we decided to include them directly as part of the train network.
Our train data includes all routes of all types (excluding Shinkansen bullet trains) within the Greater Tokyo Area. To create our network we first create route nodes and route edges from the stops and links of each route type (e.g., local, rapid, commuter express) of each line. The route nodes can be thought of as representing the station platforms for passenger loading and unloading, although they are abstracted so that distinct route types of the same line have separate nodes even if they share the same physical platform. The route edges are weighted by the mean weekday traversal time for a route link of that type on that rail segment.
We next create nodes representing each physical station in the system. Then, for each station we connect the station node to each platform node at that station via an access link with a time-weight of 3 min. The access links capture traveling between the station entrance and the platforms including congestion and waiting. Finally, we directly connect all platform nodes at the same station with a transfer link having a time-weight of 5 min. This time approximates walking times between platforms and train waiting times without overly complicating our intra-station network specification (Hibino et al. 2005).
An example of the resulting train network construction is shown in Fig. 2. There are two node types (station and platform) and three edge types (route, access, and transfer). Non-local routes (i.e., ones that skip stations) are represented as links that directly connect the platform nodes where that route actually stops (e.g., line 2 in Fig. 2). One could consider our construction of the train network as a multiplex network with station and platform nodes representing the same object at different layers and the access/transfer edges acting as inter-layer links (Kivelä et al. 2014; Bianconi 2018). However, there are no advantages to that formalism for our purposes. We simply consider it as a geographically embedded network that is abstracted to distinguish train lines that share the same station and/or platform. This construction allows us to include the walking and waiting times within each station seamlessly with standard shortest-path algorithms (described below).
Diagram of the train network construction scheme. White station nodes α, β, and γ represent the physical stations and red dashed edges represent access links connecting the station to each of its platforms. Each type of train on each train line is represented by a separate platform node (black nodes) which are connected to each other by train lines (gray) at different stations and transfer edges (blue dashed lines) at the same station. In this example, lines 1+2 and 3 run on the same tracks and both use stations α and γ, but line 3 represents an express train that doesn’t stop at station β. Only the station nodes are connected to nodes of the other transportation networks
For a network constructed in this way, the meanings and/or calculations of many standard network measures are altered. For example, because station nodes only have access links connected to them, the degree of the station nodes is the number of line types with stops at that station (40% of our stations have a single line type, so a degree of one). The degree of the platform nodes equals (1) the single access link to that platform’s station node, (2) plus the number of platforms at adjacent stations on that route (usually two, except at line termini), plus (3) the number of other line types (platforms nodes) at the same station. The platform node degrees range from 2 to 50, with 190 having a degree of 40 or more (degree distributions appear in the Additional file 1). To get the station degree corresponding to the more traditional railway representation (Barthélemy 2011) one needs to sum the number of route links connected to all the platform nodes connected to each station.
This representation also changes network path lengths because entering and exiting a station adds two jumps and every transfer adds an additional jump. As discussed later, this difference is one of a few reasons why many standard network measures, especially topological ones, were less informative for our analysis and made their values based on our analysis incommensurable with other analyses. Due to the geographically embedded nature of our network analyses, we use the sum of time-weighted edge traversals to measure network distances (i.e., not in terms of the number of edge traversals) and limit our algorithms to ones that can handle weighted graphs.
Figure 3 shows the result of constructing a rail network in this way. Train lines with only local stops can seen as sequences of blue dots connected only to the neighboring dots. A variety of rapid and express trains, sometimes multiple version on the same railway, appear as darker lines directly connecting more distant points.
Sample of the Tokyo Area train network showing lines of different types (local, rapid, express, etc.) connecting stations at different distances. Edges become darker with longer traversal times. Although station nodes are distinct from platform nodes in our construction, they share identical latitude and longitude coordinates, so they are co-located on this map view
Bus network
The bus network is constructed in the more traditional manner as links among bus stops. We still use direct links for stops of express buses even when they run the same path as a local bus. Traversal times are set from the bus schedules using the average traversal time for each link for a given type of bus (e.g., local, express). This time does not include fluctuations in road congestion, loading and unloading times, differences in speeds from skipped stops, or other interference. Unlike the train network, we do not create separate physical and route-stop nodes because bus-to-bus transfers play a much smaller role in Japanese transit. However, we found that as byproduct of this modeling choice we were unable to include wait and transfer times into the bus network, so future work will represent the bus network in the same manner as the train system.
Road network
Our road network is constructed from road segments tagged as tertiary or above, or not specifically labeled and left as ‘road’, in OpenStreetMaps data (OpenStreetMap Contributors 2019). OpenStreetMap data is sparse in Japan compared to other developed countries. Furthermore, in Japan’s fragmented and heterogeneous infrastructure it is common for roads to frequently change their thickness and allowable speeds, which complicates road classification efforts. We had to make assumptions based on typical values to fill in missing road speed limits and typical drive speeds (Japan Traffic Safety Association 2017). For approximate drive speeds we adopted a convention of 70kph for major highways, 30kph for other major roads, and 25kph for minor roads (see the Additional file 1 for more road details). OpenStreetMap data includes points between intersections to capture the bending of the road, however we simplify the network by removing all nodes from the network with a degree of two between nodes of the same road type; leaving only actual intersections. We calculate the edge traversal time based on the Haversine distance (a measure of the distance that accounts for the curvature of the Earth and the variable conversion from lat/lon degrees into meters) between intersection node and the approximated drive speed (which are slower than the respective speed limits and meant to include considerations for traffic congestion, railway crossings, turning, traffic signals, etc.).
Excluding the small local roads results in some disconnected segments and a large number of apparent dead ends as seen in Fig. 4. Although some areas are denser than others, the included roads in addition to the hexagon grid provides ample coverage of the populated areas. When we analyze the road network it is fused to the geographic hex network via connecting links. Travel along the connecting links and across interhex links fills in the gaps between intersection nodes. Although we use the walking speed of 5kph for connecting and interhex links, and 5kph is an underestimated speed even for narrow Japanese residential roads, this includes travel to and from parking spaces, congestion, waiting, and various other factors – and typically only for short distances to the nearest included intersection.
A sample of the road network superimposed on the map. Although small local roads were excluded from the road network, connections to the hex network fill in the gaps and provide dense coverage. The diagram demonstrates both the high frequency of apparent dead-ends (leaf nodes) and our elimination of non-intersection nodes. Map data Ⓒ2019 Google
Connecting links
In order to integrate two or more transportation networks we introduce links between any two nodes of different modes that are within 167m (two minutes walk) of each other. In this way transportation nodes are connected to nearby hex nodes to provide an intuitive geographic foundation for the whole system. Furthermore, when analyzed together, the nodes of other transportation networks are directly connected to each other to represent intermode transfers (e.g., from a train station to a bus stop or taxi stand – platform nodes are excluded). Like the interhex links, the time-weight on the intermode links are calculated from the Haversine distance and an average walking speed of 5 kph. The 5 kph walking speed is meant to accommodate various common factors for which we do not have data: congestion, stairs, obstacles, non-direct routes, etc.
The connecting links in our network serve the role of intermodal edges, and in many cases can be considered as actually walking from one form of transportation to another because the distances/times are based on the actual longitudes and latitudes of the respective nodes. That said, the connecting links are intended to be an abstraction rather than an approximation – although we obviously need some approximation of the intermodal change times (Ayed et al. 2011; Idri et al. 2017). All of the analyses performed here combine at least two modes (hex +…, see Table 2), and in the fully integrated network connecting links make up 17.7% of the edges, but different combinations of modes naturally require the inclusion of different subsets of connecting links.
Network summary
Although one could consider the distinct transportation modes as layers and the intermode links as interlayer edges, the nodes in each network represent different locations; i.e., a bus stop and taxi stand at Tokyo station are distinct from the station itself, which is again distinct from the many train platforms in that station. We use intermode links to represent physical travel between the single-mode transportation networks to create an integrated geographically embedded network. Because nodes are unique across modes, the network structure is identical for the layered and flat conceptualizations. We perform our analyses while treating the combined networks as simple (non-multi), non-layered, undirected graph. The node and edge counts for the components of the fully integrated network are shown in Table 1.
We use different combinations of the four transportation networks to capture five distinct travel patterns: rail, bus, driving, public transportation, and all together (see Table 2).
The hex grid provides the geographic foundation and holds the sociological data, so it must be included in all our analyses. Each travel pattern also includes the appropriate connecting links for the included transportation modes; for example, for the rail travel pattern, only connecting links between train stations and hexes are included.
Methods
Our focal analysis approach is the unsupervised learning of similar locations among 500 randomly selected hexes from the Greater Tokyo AreaFootnote 1. Similarity is determined from various combinations of measures on five different subnetworks for each of the five travel patterns in Table 2. The five subnetworks we analyse are: all nodes within 5 km as well as all nodes reachable within 20, 30, 45, and 60 min. In all cases travel times are calculated using Dijkstra’s single-source algorithm: the breadth-first summation of traversed edges’ time-weights (Hagberg et al. 2008).
As an example of both the differences among modes and large scale of the subnetworks, Fig. 5 shows the travel times and extent of travel within 60 min from the hex including Tokyo Station for the rail (top), bus (middle), and driving (bottom) travel patterns. Rail travel produces a signature dappled pattern of walking times radiating from stations. Suburban stations with express trains are easily identifiable as clumps of hexes that are greener and larger than their neighboring stations, while the central region has a more diffuse pattern due to the high density of stations and tangled collection of routes. Due to the close proximity of adjacent bus stops, the bus network shows a smoother radiating pattern from the city center, but also islands of reachable hexes where express buses make connections. The driving pattern yields the widest extent and the most even coverage with major highways creating tendrils of higher-speed travel into the suburbs.
For each of the distance/time and travel pattern subnetworks we compute a battery of scores based on network and geotemporal measures. These scores are used (1) directly to sort and characterize the neighborhoods, (2) are combined to produce scores for higher-order features, and (3) are the fuel for machine learning techniques to cluster and compare these locations.
Network measures
Our most basic evaluation utilizes the following standard network measures applied to each subnetwork: number of nodes, number of edges, the eccentricity of the focal location node, the closeness centrality of the focal location node, the mean degree centrality, the mean eigenvector centrality, and the number of nodes on the boundary of the subnetwork. All of these measures were calculated using the time-weights of the edges where appropriate.
Network measure descriptions
Because our network is a simple (non-multi), flat (non-layered), undirected weighted network the measures we use are the familiar ones (Newman 2003) included in the NetworkX Python package (Hagberg et al. 2008). For each of the travel patterns, the number of nodes and the number of edges are inclusive of the modes for that pattern. For example, the public transportation pattern includes the train, bus, and hex networks as well as connecting links binding them together; thus the number of edges includes train access, transfer, and route links, plus the bus links, plus the hex links, plus the connecting links within that subnetwork. With ki representing the number of neighbors (of any kind) of node i and NS being the number of nodes in subnetwork S, the mean degree centrality of a location equals
The sole exception to our use of time-weighted measures, the eccentricity of focal location node i is the number of edge jumps from i to the furthest node in its subnetwork. Because the furthest distance in meters/time is set by the subnetwork-creating parameter (5 km, 20 min, …) this becomes a measure of network efficiency that captures the linkage structure to achieve that distance (especially for the 5k case).
Although we use the Wasserman and Faust version of closeness centrality, because all subnetwork nodes are reachable from the focal location it is equivalent to the original Freeman formulation (Hagberg et al. 2008). For focal hex node i the closeness centrality is the number of hexes in the subnetwork divided by the shortest distance weighted by traversal time d(i,v) to each reachable hex v.
This gives higher scores for more compact and densely connected subnetworks with the idea of comparing locations when subnetworks are made using the same distance/time parameter.
Eigenvector centrality measures the influence of a node by increasing a node’s score the more it is connected to by highly connected nodes (Newman 2003; Hagberg et al. 2008). Instead of using the eigenvector centrality of the location hex node, we calculate the eigenvector centrality of each node in the relevant subnetwork (with a tolerance of 0.001) and use the mean value to characterize the subnetwork.
Boundary nodes are those not in the subnetwork but connected directly to nodes that are in the subnetwork. This is akin to a measure of the perimeter size or circumference of the reachable area, but it accommodates irregular shapes. It does not count hexes along the coastline or boundaries (because there are no hexes further out), so it is biased toward central, inland areas.
Exclusion of specific network measures
There are several other measures of network structure that are useful for characterizing and comparing single-mode transportation networks (Guimera et al. 2005; Crucitti et al. 2006; Derrible and Kennedy 2009; Barthélemy 2011; Derrible 2012; Rodrigue et al. 2016). Initially we intended to use a “kitchen sink” approach including a much larger set of measures including betweenness, diameter, degree distributions, clustering, Wiener index, and the number of communities. However, we were forced to exclude these and other measures due to their prohibitive computational requirements and/or their inappropriateness for our geographically networks.
As an example, consider the betweenness centrality of the 5 km subnetwork of any given location. We could choose either the betweenness centrality of the location’s focal node or an aggregate (mean/max) of all the nodes in the subnetwork. As for the betweenness of the focal node, recall that all location nodes are hex nodes, and travel along any transportation edge is faster than the walking-speed hex and connecting links. As a result, the focal hex will only be on a shortest path when walking is the fastest way to cross through the center of the region. That case can only occur when there are few to zero transportation links running through the region. We directly measure the number of transportation nodes/edges, so this measure is uninformative given the structure of our integrated network.
The mean or max (or max −mean) betweenness should tell us whether there are bottlenecks and/or high-throughput corridors for the traffic within the region. High betweenness scores are expected among highway intersection and train station nodes, but these make up a small fraction of the nodes in any subnetwork so mean values would fail to differentiate locations. Furthermore, we would be measuring betweenness only among points within the subnetwork, not the full transportation network, so there is no clear useful interpretation of the score. For example, some location may include the world’s busiest train station (Shinjuku station) at the fringe of its subnetwork, but within that subnetwork it would still have a low betweenness score.
One alternative is to calculate the betweenness scores (and other measures) for all nodes in the full network and aggregate them within each subnetwork, but with 360,977 nodes and more than a million edges the computation was impractical. The other measures were excluded for similar reasons. Due to the high connectivity of the hex network, the clustering coefficient is high across the network. Also due to the hex network, graph communities can only form when there are express trains/busses/highways with long edges (as in Fig. 5 top and middle), but the number of such communities does not correspond to any intuitive feature of the transportation networks for a region. If we want the presence/impact of long-range edges we can directly aggregate the edge lengths within a subnetwork. It should be noted that the interpretation of some of the included measures is also affected by the hex network, as is discussed in more detail in the results section.
Geotemporal measures
In addition to the measures from network theory we include specifically geographic and transportation-focused measures. For each subnetwork we determine both the number of hexes and the number of people within the subnetwork. The number of hexes is naturally similar to the number of nodes above (especially because the hex nodes are always by far the most numerous), but counting only the hex nodes provides a fairer comparison of the transportation modes’ ability to access an area. Counting the hexes is equivalent to measuring the area because each hex covers the same amount of space. Each hex contains the population of its covered area, so the number of people is simply the sum of the populations of the hexes included in the subnetwork.
Although the numbers of hexes and people are rough measures of accessibility, we also include time-weighted versions: reachability and sociability respectively. We measure the reachability of a location i as the time-weighted number of hexes reachable from i within the constraints of a given subnetwork (5 km, 20 min …). Specifically, the reachability of hex i is calculated by
in which tij is the shortest time in minutes from hex i to each hex j in subnetwork NS (we use tij=1 when i=j). Inversely weighting by time produces a measure that discounts far-off locations so that greater connectivity to transportation networks near the focal location i is more strongly rewarded. That is, being far from a major station or next to a minor station may generate similar numbers of hexes within a certain time horizon, but we can differentiate these cases using the reachability measure.
In a similar vein we use the population data to determine the sociability score of each location defined as the number of people who can reach each location weighted by the time it takes to reach it. We simplify and generalize the measure from (Biazzo et al. 2018) to handle continuous travel time values and averaged edge traversal times. Specifically, the sociability score for hex grid location i is calculated as
in which Pj is the population of hex j and tij is again the shortest time in minutes from hex i to hex j.
For each subnetwork we also determine the furthest point from the focal location. This requires a different measure for distance-constrained vs time-constrained subnetworks. For the 5 km subnetwork it is the longest travel time; i.e., how long it takes to reach the most remote hex within the area. It is thus a measure of the spatial efficiency of the region. For the 20, 30, 45, and 60 min subnetworks it is the distance to the furthest hex reachable in that amount of time. It is often possible to reach additional transportation nodes even further out, but we only consider hex nodes in this score.
Custom combined measures
Up to this point we have a total of 300 measures for each hex: 12 network measures ×5 subnetworks ×5 travel patterns. We also combine these core measures across subnetworks for each hex to reveal higher-order features for comparison and clustering. Here is where we try to ascertain more sophisticated accessibility features such as the relative efficiency, interplay, and dominance of modes of transportation.
Network synergies
By subtracting the number of hexes from the number of nodes we recover the number of transportation nodes, which is useful in discerning a location’s mode-dependencies and the synergistic effects of multiple transportation modes. We evaluate the degree to which combining networks amplifies their efficacy by comparing selected measures of the rail+bus and rail +bus+driving networks compared to the rail, bus, and driving networks separately. Figure 6 shows one example of how combining the rail and bus networks facilitates greater accessibility.
In this case the combined network can reach further and more places within 30 min than either single network, demonstrating the synergistic effects of multi-modal transportation networks. Some locations exhibit strong synergistic effects, while others are dominated by one of the transportation modes such that adding another does not expand the reachable area.
There are three aspects to our measurement of network synergy. First we measure saturation synergy using the number of transportation nodes in the combined network divided by the sum of transportation nodes in the individual networks. Using the travel pattern subnetwork symbols from Table 2 focused on hex i and nt, nb, and nr to refer to nodes of the train, bus, and road modes respectively we have
We measure distance synergy of location i using the ratio of the Haversine distances to the furthest reachable hex of the combined networks over the max of the individual networks. Letting dmax(NSi)= maxjd(ni,nj),nj∈NSi; i.e., the furthest point nj from the focal hex node ni in subnetwork NSi, we have
We also evaluate improved connectivity within the region (i.e., gaining heavier weights near the focal location) by calculating reachability synergy and sociability synergy using similar calculations as distance synergy. Using \(\mathcal {R}(N_{Si})\) for the reachability and \(\mathcal {S}(N_{Si})\) for the sociability of subnetwork NSi of location hex node i these synergies are calculated as follows:
For simplicity, in the current work we only perform these synergy measure calculations for the 30 min subnetworks.
Mode centricity
Because for every location we expect the road network to facilitate the greatest accessibility by all measures we evaluate transportation mode dominance in a relative manner. Specifically, for each measure \(\mathcal {M}\) of the 30 min rail subnetworks, we divide it by the corresponding measure for the bus, and repeat that for the driving travel pattern. We also take the bus subnetwork values divided by the driving subnetwork values to complete all pairwise competitions. In the current paper we use this measure to assess travel mode dominance, and for this reason we limit its application to the following variables: reachable hexes, reachable people, reachability, sociability, and furthest point. As a result, each location has 5 values for each of three comparisons: Rail |Bus, Rail |Driving, Driving |Bus.
We can use these scores to directly measure the relative usefulness (and hence dominance) of each location and to cluster the locations by similar relative values.
Summary of measures
The twelve measures in listed in Table 3 applied to the subnetworks generated by each of the five travel patterns (Rail, Bus, Driving, Public Transportation, All) for the five distance/time parameters (5 km, 20 m, 30 m, 45 m, 60 m) gives us 300 core measures from network theory and geotemporal analyses. We further add the combined measures listed in Table 4 to the core measures as well as additional variations introduced below.
As noted earlier, we initially intended to include more core measures from transportation analysis, network theory, and geotemporal studies and other combined measures. These measures were removed from our list either because they were computationally impractical, could not be given and intuitive/useful interpretation for our network construction, or were not revealing of interesting geospatial patterns. Our inclusion of the spatially explicit hexagon network, a feature absent from most previous work (c.f. Biazzo et al. (2018)) but necessary for our purposes, causes most of these issues. Not only does the hex network greatly increase the number of nodes and edges in the system, its lattice structure makes interpreting measures such as degree centrality and clustering coefficient less straightforward. Although we computed several additional measures that we could add into the mix (e.g., population centrality, population scaling, 60m |30m measure scaling), the core measures plus our selected combined measures suffice for enabling our classification of locations using machine learning.
Machine learning techniques
In addition to providing a profile of the multifaceted transportation system, the network and geotemporal measures above are also fuel for our clustering and dominance analysis. Much like our evaluation of network measures used in previous transportation network analyses, we found that previous work on network similarity and structural profiling (Soundarajan et al. 2014) became unusable or inappropriate for our model/purposes. Specifically, previous network similarity measures depend on calculating features of the network that are either too computationally expensive or that fail to reveal characteristic features of our networks (again mostly due to the inclusion of the hex network).
For example, measures of whole-network similarity like NetSimile (Berlingerio et al. 2012) and Normalized LBD (Richards and Macindoe 2010) depend on collections of measures of the micro-structures of the network. Graphlet methods (Pržulj et al. 2004)) similarly depend on the frequency of particular motifs within a network to act as a profile or fingerprint to measure similarity. However, structures like cliques and trees among small numbers of nodes are not predictive of accessibility, speed, and reach of travel. Also, the geographic nature of these transportation networks implies bounds on the frequency of certain structures that do not exist for social and other networks. Finally, the inclusion of the hex grid and connecting links, and even just the inclusion of multiple kinds of links makes these techniques difficult to apply and/or interpret.
Clustering algorithms
As a result, instead of relying on existing network similarity and profiling methods to act as a metric for clustering, we rely on standard unsupervised machine learning methods applied to the core and combined measures for each location. We first standardize each measure on the [0 1] range using (xi− minx)/(maxx− minx) to improve the performance of distance-based clustering methodsFootnote 2. By combining our data in different ways we create several different experiments (described below) to uncover clusters for a variety of location characteristics.
In order to more easily compare the results of multiple clustering algorithms and experiments we decided to fix the number of groups to seven. The motivation for clustering into seven groups derives from the train vs bus vs road tricotomy and our interest in mode comparisons. With three poles there are 7 possible dominance combinations: train, bus, road, train + bus, train + road, bus + road, and all three being even. Although not all of our analyses are about dominance, and we don’t expect all the results to fall neatly into these particular groups, we needed to choose a number of groups and this is why we chose seven (in addition to being a nice medium-sized number for our dataset).
For each set of variables we apply three common unsupervised learning techniques: K-means, hierarchical (agglomerative) clustering, and spectral clustering from Python’s Scikit-learn package (Pedregosa et al. 2011). Although other clustering methods could be applied to the data, we limited ourselves to ones that (1) include a parameter for the number of clusters, (2) output partitions of the data (no outliers), and (3) are sufficiently performative on our data.
For K-means we used Scikit-learn’s default parameters except for the number of clusters. Because our data is dense, the Elkan algorithm is used, run with 10 seeds for 100 iterations, and with a tolerance of 0.0001 (Pedregosa et al. 2011). For spectral clustering we used the nearest neighbors affinity parameter and seven clusters, and the default values for the other parameters (Pedregosa et al. 2011). For hierarchical clustering we used a bottom-up agglomerative clustering approach with seven clusters and the “average” linkage parameter; the defaults were used for the remaining parameters (such as Euclidean affinities and no distance threshold) (Pedregosa et al. 2011). Our primary interest here is differences in clusters from considering different specific subsets of our data, so we only briefly investigate the differences in clustering results for these three approaches using mostly the default parameters. Future work on more specific clustering goals may explore tuning additional parameters to achieve improved categorization for those narrower purposes.
Comparing clusterings
We compare the results of different clustering algorithms and the results of the same algorithm on different datasets using the AMI score (adjusted normalized mutual information score, henceforth “mutual information” or “AMI”)(Vinh et al. 2010). Although we also examine the adjusted Rand index and the percent similarity in the label assignments, these are largely redundant with mutual information and thus not included in the results below.
All algorithms are set to find seven clusters, but the sizes of the clusters are heterogeneous. Some clusters may have just one or a few members (especially with hierarchical clustering) and this can be interpreted as the number of clusters found by the algorithm being fewer than seven. We can evaluate the diversity of the cluster sizes using a measure of the effective number of groups; and we use the inverse Simpson index following (Laakso and Taagepera 1979):
where pi is the proportion of the locations in group i. If all clusters are of equal size, then the result is 7. As the heterogeneity in the group member counts increases the value moves closer to one. Unlike simply measuring variance, this has the additional merit of providing an intuitive interpretation. For example, if two groups are nearly empty and the others are roughly even, then it informs us that there are effectively five groups.
To ease the intuition of reading our clustering result diagrams we want to match clusters to the same group number as much as possible, and this requires a measure of label similarity. To assign label similarity scores we first sorted the labels of the k-means results of each experiment by the mean of the values of the cluster centers (across all included dimensions). We then mapped the labels of the other two clustering methods to the k-means labels using the Python Munkres package version of the Hungarian algorithm (Clapper 2008). In this way, clusters with similar data values will be assigned the same label number for all three clustering methods. These shared labels are used both to identify which locations are classified differently and to maintain consistent group colors for plots. However, this process is not completely consistent in assigning labels because differences in included points can sufficiently change the centroid values to make label similarity impossible (and meaningless – if the clusters have widely different members then they fail to be similar enough to merit similar indices anyway). Because mutual information is not sensitive to the labels it is adopted for quantitative cluster comparisons but is less useful for visualizing the differences in results.
We also want an intuitive way to judge the meaning of the clusters (i.e., which kinds of locations are grouped together). The large dimensionality of our dataset makes any simple summarizing inadequate. Ideally we would like to see the n-dimensional space to evaluate the goodness of fit and understand the meanings behind the discovered clusters. Because of the large number of experiments performed, in lieu of a highly detailed and focused investigation into a particular cluster’s features we make use of a simple measure to characterize each cluster. For each node we calculate the mean value of all the variables included in an experiment, and then we again standardize those values on the range [0 1] to make the differences clearer. We use this value as the circle size in plotting results to get some idea of the relationship between the values of the features and the cluster membership of each location.
Results
With a dataset as rich as this, the collection of methods that we could use, and the collection of experiments we could run, is excessively large. As such, many of the analyses we performed are not covered in this treatment. We narrowed it down to those which we judged to be most revealing for our substantive questions after broad preliminary investigations.
Feature correlation
As previously explained, we excluded some network measures because they were computationally too expensive or uninformative for our network construction. It is also advantageous to exclude measures that provide redundant information. In consideration of space and focus, we omit the details of our feature selection/dimension reduction analysis. However, we briefly examine the correlation levels among the core measures because they also reveal important differences between our network construction and most previous analyses of transportation networks.
We assess the similarity in the core measure correlation matrices using the standardized Frobenius norm of the difference between two correlation matrices. With twelve variables ranging from −1 to 1, the maximum difference is 24, so we divide by that number to get the proportion of possible difference. All pairwise comparisons grouped by travel pattern and distance/time threshold are available in the Additional file 1 while Table 5 presents the mean values by travel pattern (left) and by distance/time threshold (right). We find a high level of similarity in the correlation levels across transportation modes; e.g., the mean difference in the correlations of the core measures across all 500 locations and across the five distance/time thresholds for the train + hex subnetworks is only 5.6%. Among the distance/time aggregates it is unsurprising that the 5 km has the highest level of correlation similarity because the hex grid is indistinguishable and dominant within 5 km (excepting locations along the boundaries). We also find that similarity decreases with increasing time radius as should be expected.
A similar correlation pattern exists across all the travel patterns and subnetworks, which reflects the purpose-oriented and physical constrains of transportation networks. However, the differences that do exist tell us that these 12 core measures do capture a profile that is distinguishable for each travel pattern and distance/time threshold. There is one notable difference that we can highlight using the two correlation matrix plot samples in Fig. 7 (correlation plots for the other subnetworks appear in the Additional file 1): the 5 km and distance-based subnetworks have specifically distinct correlation patterns. Recall that the furthest point measures has different definitions for distance-based and time-based thresholds. The reason for this is clear when we examine the correlation matrices: the distance to the furthest location for the 5 km case, and the longest travel time for the time-based cases, are uncorrelated with anything because they are nearly or exactly constant. It is because these measures are useful in mutually exclusive cases that we collapse the two measures into the single furthest point measure.
Correlation matrices of the core measures on the fully integrated travel pattern within 5 km (left) and 30 min (right) across locations. Figures for other travel patterns appear in the Additional file 1. For each travel pattern the correlation pattern is consistent across time threshold, so only the 30 min matrix is shown
The numbers of nodes and edges are nearly perfectly correlated in every case as one would expect (note that the numbers of nodes and edges are dominated by the hex network). Most of the measures are consistently positively correlated with the number of nodes across networks and subnetworks, with mean degree centrality and eigenvector centrality being typically anti-correlated. Eccentricity and the furthest point are negatively correlated for the 5 km subnetworks, but are both positively correlated for the time-threshold subnetworks. The measure with the most volatility is closeness centrality (which is sometimes positive and sometimes negatively correlated for the same travel pattern at different time thresholds); however it is also weakly correlated with the other measures. None of these patterns are surprising when we carefully consider the construction of the network and features being measured.
For example, it may be at first counter-intuitive that reachability would be anti-correlated with mean degree centrality; after all, the more transportation connections there are, the more places one should be able to access. However, most nodes in the hex network have a degree of 6 (98.6%), which is larger than the degree of 99.9% of road nodes, 81.7% of station nodes, 42.5% of platform nodes, and 98.3% of bus stops. Thus the presence of more transportation nodes increases the reachability (as expected) while decreasing the mean degree because the degree of the transportation nodes is typically less than the hex nodes. If we isolate the degree to only among non-hex links, then a greater mean degree would correlate with larger and further-reaching subnetworks. But the inclusion of the hex network changes this relationship so that higher values (i.e., closer to six) indicates fewer transportation nodes, and hence lower reachability.
Eccentricity is nearly always positively correlated with the number of nodes for the time-threshold subnetworks, but is always negatively correlated for the 5 km subnetworks. This is because for the 5 km case more nodes/edges always means more transportation nodes and therefore fewer edge jumps to reach the perimeter: more nodes leads to lower eccentricity. However, for the time-threshold subnetworks more nodes almost always results from a greater range, and this typically requires more jumps to reach the furthest edge.
Closeness centrality’s correlation is the most volatile across time-threshold subnetworks and across travel patterns. Recall that closeness is calculated as the number of nodes in a subnetwork minus one divided by the sum of the time-weighted distances from the focal hex to each node in the subnetwork. For the 5 km cases, more nodes means more transportation nodes, hence more connectivity and shorter travel times within the region, and therefore greater closeness centrality of the focal hex: they are positively correlated. As one can see from Fig. 5 (top), train travel is only efficient along the tracks, so the number of reachable nodes does not increase as fast as the time to reach the further nodes, making closeness and the number of nodes negatively correlated. Figure 5 (bottom) also shows how the reachable nodes for driving subnetworks expand radially; as a result the number of nodes and the distance to those nodes increase together. The rate of increase in the number of nodes (numerator) and distances (denominator) turns out to be similar, and as a result the closeness centrality for the driving subnetworks is not strongly nor consistently correlated with anything.
The above analysis of the correlation patterns is meant to highlight differences in the measure relationships resulting from our geographically embedded network construction and between distance- and time-constrained subnetworks. The discovered patterns reveal that each subnetwork has a distinct signature, but that the differences across time-thresholds for the same travel pattern are small (≤7.74%). We additionally used these correlation patterns to select measures to include in the experiments described below.
Geospatial patterns in transportation network characteristics
Here we examine the spatial distribution of the groups found by clustering and how they differ by clustering method and included measures. There is no ground truth regarding which category a location should be in or which locations should be grouped together. As such there is no metric for how correctly an algorithm clustered the locations. Instead, our exploratory analysis aims to uncover relationships between the characteristics of the hexes, their surrounding area, and their locations on the map.
All core measures
We first present the results of clustering the 500 locations using all 300 core measures (12 measures ×5 time-thresholds ×5 travel patterns). Because this analysis combines all five travel patterns and all five subnetworks for each location, it acts as a broad-stroke baseline characterization of the locations. Figure 8 shows the clusters found via k-means and hierarchical clustering (spectral clustering omitted for space, available in the Additional file 1). Figure 9 shows the number of locations per group (left) and the mean value per group (right) by clustering method. The k-means and spectral algorithms generate separate groups among locations with similar characteristics (especially in the outskirts) while grouping locations with different features together (especially in the city center). Hierarchical clustering, on the other hand, leaves two groups essentially empty to create five groups that are more diversified in values.
Clustering into 7 groups using k-means (top) and hierarchical (bottom) methods using all 300 core measures collected. Marker size corresponds to the mean value across the variables and colors represent the cluster number. There are clear and important differences in the clusters found between the two methods. Map data Ⓒ2019 Google
Due to the differences in group sizes the effective number of groups for k-means is 5.97, but only 1.75 for hierarchical and 4.05 for spectral clustering. Hierarchical clustering creates groups with just 6 and 2 members for the greatest two mean values, and these accurately separate the most central locations into intuitively different classes (near and not-so-near major stations). Locations near secondary city centers are among the 14 members of the next category. More than 200 locations are binned together yet a single location makes up a group with a similar mean value. This single location truly is an outlier (the blue dot in the southwest corner out in the water in Fig. 8) so it is reasonably different in its measure values from all other nodes.
Whether a finer breakdown of suburban and rural areas (k-means and spectral) is preferred to a finer breakdown of central locations (hierarchical) is a matter of preference. Note that although clustering in 300 dimensions could reveal clusters that align in unimaginable patterns, due to the high correlation of the variables, all clustering methods generate groups in a roughly concentric ring geographic pattern. The Pearson clustering coefficient of the mean value of the 300 variables and the location’s distance from Tokyo Station is -0.683Footnote 3. By exploring the core measures and various combinations of these core measures we uncovered many patterns that are useful for better understanding accessibility quality around the Greater Tokyo Area. For now, however, we move on to specific analyses directly related to accessibility and clustering.
Reachability and sociability
Reachability and sociability are highly related measures: reachability aggregates the time-weighted area and sociability aggregates the time-weighted population of that area. There is a key difference, due to the inclusion of the hex network the reachability of a location is always strictly positive, while sociability can be zero. Figure 10 shows the reachability and sociability values for each location for each travel pattern using the 5 km and 60 m subnetworks. The 5 km plots clearly reveal this difference: there is a dense line around a reachability of 45 representing regions requiring a lot of walking from the focal location; lower values indicate locations near a boundary.
Reachability and sociability scores for each location broken down by travel pattern for the 5 km and 60m subnetworks. The patterns reveal similarities and differences between these geotemporal measures as well as demonstrate the role of synergy and the overall dominance of the road network discussed in detail later
For the 5 km subnetworks, rail travel is the weakest for both reachability and sociability, followed by bus and public transportation (rail + bus), while driving and the fully combined network have the greatest (and roughly equal) distribution of values. Examining the 60m subnetworks reveals two interesting differences: (1) the best rail values are superior to the best bus values, and (2) public transportation is notably superior to both the rail and bus networks that it is composed of. The latter result comes from mode synergy, which we discuss in detail below. It is also clear that including the road network systematically enhances both reachability and sociability, which is discussed below regarding dominance.
Here we want to reiterate that trains are very fast once you reach the station, but they only foster travel along the tracks. Bus networks are more dense and pervade more areas, so on average they provide greater reachability; however, some areas (esp near the city center) have very high rail connectivity and these areas can out-compete bus reachability (Fig. 10 bottom-left). Moreover, these central areas with multiple convenient train lines provide access to many densely populated suburban areas, so within 60m the train sociability is even more competitive with buses than the reachability (Fig. 10 bottom-right).
We now turn to investigating the groups formed by reachability and sociability. Table 6 summarizes the mutual information of groups averaged across travel patterns for each clustering method. The key results here are (1) by all clustering methods, sociability similarity is much higher than reachability similarity, (2) the 5 km subnetworks are more similar than the 60m for sociability, but not consistently so for reachability, and (3) the particular comparisons giving the min and max values vary greatly among methods and subnetworks. For point (3) we simply note that the same All vs Driving comparison yields the lowest sociability similarity for 5 km subnetworks, but the highest similarity for 60 m subnetworks. A more in-depth analysis is not revealing of general patterns so is left out of this paper (more comparison details are available in the Additional file 1).
It is surprising to find that sociability similarity is much higher than reachability similarity, especially on the 60m subnetworks, because the two measures are so related. Spectral clustering in particular produces an anomalous level of dissimilarity for the 5 km reachability scores (0.0405 on average). We examine this more closely by looking directly at the relationship between the two variables. Figure 11 shows the correlation and the mutual information of group members formed by clustering on reachability and sociability values. From it we can see that k-means produces the most similar pattern to the correlation levels for both subnetworks, followed closely by hierarchical clustering (which consistently generates more similarity for public transportation), while spectral clustering yields rather dissimilar results. Although producing similarity levels matching correlation has an intuitive appeal as a reality check for the accuracy of a clustering method, it is not a full-fledged benchmark. The correlation between reachability and sociability for the 60m subnetworks is 0.956, and we are clustering on just one variable here, so the clustering methods only need to find appropriate divisions for both variables to match up the groups. In consideration of that all the clustering results are lower than expected. This could be a result of the parameters used for clustering, but more likely it is a feature of the data: despite being highly correlated, the reachability and sociability variables are clumped differently, and therefore put different locations in different groups.
The correlation and group member mutual information between reachability and sociability for selected subnetworks. Tabular data available in Additional file 1
Network synergies
One of our custom geospatial measures is the degree of transportation network synergy among the different modes. In contrast to determining which mode of transportation is dominant, the network synergies reveal interplay between the modes that reinforce each other. We are particularly interested in synergies for public transportation access; i.e., improvements in accessibility from the joint use of trains and buses. The most obvious benefit of joint usage is for locations far away from their closest station. Trains, especially express trains, are excellent methods for reaching distant points. But if a location is far from the station then the walking time can drastically reduce the usefulness of the train network. In many such cases there are bus routes dedicated to bringing people to the station.
Based on our measures of synergy, a location will have a value of zero if no nodes of one type exist, a value of 1 if there is no synergy (i.e., the joint value is no better than one of the components), and larger values from there based on the proportion of added benefit generated. Figure 12 shows locations with similar public transportation synergy levels according to hierarchical clustering (colors) along with their level of synergy (size).
Public transportation synergy scores (sizes) and groups via hierarchical clustering (colors). Size represents the mean of the four synergy measures, so the small purple dots indicate a score of 0 (no trains, sometimes no buses either). Although the regions of similar synergy levels are scattered geographically, regions of low synergy may indicate areas where increased bus service could substantially increase reachability
The Rail +Bus+Driving synergy values tend to be significantly higher than the Rail + Bus synergies because the road network is the most expansive and dense (excepting the hex network, of course). If we think of the road network as taxi usage, then this confirms how much more convenient trains (and even buses) are if we can take a taxi to them from our homes. We perform two analyses to test the idea that distance from the station or bus stop plays an important role in the synergy levels. First we examine the correlation of the distance to each kind of transportation node to each synergy score separately in Table 7. Negative values for each relationship means that being closer to the nodes creates greater synergies. We actually expected Rail + Bus synergies to be higher when further from the station, but this result implies that the combined network reaches more people because of bus use to spread more diffusely away from each station. We also expected that the distance to the nearest intersection would have the lowest synergy values because the furthest distance from a location to its nearest intersection is less than 1750m (compared to 12 km for the furthest train station).
Instead of looking at the individual correlations, we can examine the combined explanatory effects simultaneously using a simple regression model. We computed the R2 values of a linear model of the distances to each of the closest nodes of the relevant types to the synergy measures. The results in Table 8 tell a similar story to the correlation results, but with a twist. The distances do not have an appreciable effect on distance synergy (the furthest reachable distance) and only a minor effect on reachability synergy. As expected, the distances to the transportation nodes produce a weaker effect for the Rail +Bus+Driving synergy measures than Rail + Bus because nearly every location is near an intersection node. Sociability synergy is so much less when including the road network because the places one can go via car, but not via train or bus, are places where considerably fewer people live.
Although these synergy measures and statistical analyses are extremely valuable for our interests in accessibility, the clustering results are somewhat less useful. Figure 13 shows (via color) the clusters found by each algorithm. Not only do the synergy values not form cohesive geographical patterns as seen in Fig. 12, but they are also highly mixed when viewed as related to distances to the nearest transportation nodes. There are noticeable clusters in the plot, as we expect from the correlation values, but it is still unclear how to use the synergy cluster information to gain a better understanding of accessibility. We may develop a better understanding of the factors leading to high synergy in follow-up research that analyses every hex instead of selected locations.
Scatterplot of the relationship among the distances to the nearest train stations (x-axis) and bus stops (y-axis), the mean of the four train-bus synergy scores (size), and the group membership for each clustering method (color). Zoomed into distances within 3 km (plots of the full range appear the Additional file 1)
Transportation mode dominance
We utilized multiple approaches to identify regions with similar dominance patterns. The first approach is to simply group the locations using all the measures we defined for this purpose: the pairwise mode comparisons of reachable hexes, reachable people, reachability, sociability, and furthest point for the 30 m subnetworks (described above). This allows us to cluster locations by the relative strength of their transportation modes. For example, clustering on the reachability comparison measures puts together regions without trains and buses, ones with buses and no trains, areas that are strong in all three, and areas with particularly strong trains. Figure 14 shows that our experiments using clustering methods to identify areas with similar transportation mode dominance patterns met with only partial success.
Locations with similar profiles are scattered throughout the area so they must be bound by other features of the locations. A hex that happens to be far from its closest station is going to have a weak train strength, and whether it is dominated by road or bus will depend on whether any bus lines run nearby, for example. A different hex, maybe just one kilometer away, could be one kilometer closer to the same station, and that difference may make the train network extremely useful. That local difference in the relative usefulness of each transportation mode drowns out any large-scale geographic pattern.
To test this hypothesis we also investigate the relationship of the comparison measure values to the local mode-dependent accessibility. First we calculate the distance from every hex to its closest train, bus, and road network node. We use these distances to perform both a correlation analysis and a clustering comparison, so we also group the resulting distances into 7 groups using the same three clustering methods. Next we introduce three new measures to explicitly measure dominance based on the non-standardized core measures. Letting \(\mathcal {L}\) be the list of measures we use to assess dominance (reachable hexes, reachable people, reachability, sociability, and furthest point) we have
We eliminate rows with a 0 or 1 value for any of the comparison measures to ensure real values, leaving 355 of the 500 locations. Using these dominance measures we revisit the relationship between distance to the nearest node and mode dominance.
The Pearson’s correlation between the rail dominance measure and the distance to the nearest station is −0.168; indicating that being near a station contributes only slightly to rail travel being important for that location. Similarly, the correlation of bus dominance to the nearest bus stop distance is only −0.199. However, road dominance has a much lower correlation (−0.073) with the nearest intersection. The level of mode dominance likely depends on many nuanced features of a location’s transportation network, but access to transportation systems must be important.
As an alternative to correlation, we examine the similarity between groups created by clustering on the dominance measures and clustering on distance to the nearest transportation node of the relevant type. Table 9 summarizes the mutual information between these groups. Note that the values are low (AMI ranges from roughly 0 for independent clustering and 1 for identical clustering), perhaps indicating that similarity of discovered groups may not be an effective method for evaluating the relationship between two variables (at least with the current set of parameters). Actually, this only confirms that the two features are not as connected as our intuition would have us believe. The dominance measures include the relative strengths of five sophisticated geotemporal measures that depend on many complex and idiosyncratic features of the integrated transportation networks. It is thus not surprising that no single variable, however intuitively linked, would provide strong explanatory support on its own.
Figure 15 shows the geographic distribution of the rail dominance score groups according to hierarchical clustering for the 355 remaining locations. There is a partial geographical pattern that is revealed in the correlation of the dominance scores to the distance from Tokyo Station: rail dominance is 0.287, bus dominance is −0.067, and driving dominance is −0.227 (a scatterplot of these relationships is available in the Additional file 1). These results reverse the pattern we see from other analyses and our expectations: rail is most powerful far from the city center, driving is most powerful in the center and suburbs, and buses are widely dispersed and evenly spread out. We find the largest rail dominance in remote areas like valleys serviced by trains where there are no buses and only slow winding roads that run parallel with the tracks. For our purposes of scoring locations and evaluating their reliance on particular modes of transportation, the specific dominance scores (i.e., the values within groups) are valuable information while the clustering of locations by their dominance is underwhelming. In particular, clustering by all the dominance scores together, the analysis that motivated our choice of 7 groups for clustering, puts nearly all the nodes in the same category, leaving remaining groups filled with one or two exemplars.
Clustering method comparison
In total we perform k-means, spectral, and hierarchical clustering on 61 different subsets of our core, combined, and extended measures (our experiments). For each experiment we calculate the mutual information for each pair of methods. A table with the full list of comparisons appears in the Additional file 1; here we highlight some points. Our project is to apply these methods to reveal substantive features of our data rather than to evaluate methods, and as such we have no ground truth nor any other yardstick by which to judge the accuracy of these methods. Furthermore, we did not perform sensitivity analyses nor parameter sweeps to optimize the application of these techniques to some independent desiderata. That is simply not our project here. However, we do evaluate the differences among the methods because understanding how and where they differ is important for interpreting the results and choosing methods for future work.
Table 10 summarizes the pairwise comparisons of the clustering methods. As one should expect, k-Means and spectral clustering produce similar groups on average, and they are more similar when a large number of variables are included. The high average similarity between hierarchical and k-means clustering is initially a bit surprising; however, 28 of the experiments involve only one variable for one network and one subnetwork and the results are similar in those cases. We also did not expect spectral clustering to be more dissimilar to hierarchical clustering than k-means. Because our locations were chosen randomly, there is no reason to think that the values of our measures would be tightly grouped (and they are not). We expected that spectral clustering would find oddly-shaped groupings in high dimensions more similar to those of hierarchical clustering, but this is not the case. Spectral clustering mismatches hierarchical clustering more, rather than less, when few variables are used and this likely explains the unexpected cluster matching.
Correlation provides an intuitive guide to similarity that we can use to evaluate the similarity in groups generated by the different clustering methods. For example, we find that spectral clustering produces anomalous and inconsistent results on the comparison of reachability and sociability. Correlation and regression analyses can be used to augment or replace the use of clusters for our broader applications. Despite this, a more detailed investigation into which clustering methods (and parameters) are appropriate for which datasets is intended for future work because it holds the potential to categorize locations across multidimensional data without requiring us to develop sophisticated scoring equations.
We found that using seven clusters provided intuitively reasonable breakdowns of areas in many analyses, especially for hierarchical clustering (which will leave a group essentially empty if a good division with fewer groups is found). However, we also found that more distinctions could be made in some cases. For example, in Fig. 8 the k-means method distinguished inner and outer suburbs that hierarchical clustering did not, but then it grouped noticeably distinct city center locations together. Both methods generated useful clusterings, and so we are considering an ensemble approach for future studies that both combines these three methods and also includes a sensitivity analyses for the number of groups. Because we do not have a basis for what is the correct categorization beyond intuition and cross-checking, identifying locations with consistent vs inconsistent classifications across methods and parameters can be used as a kind of bootstrapped confidence in the clustering results.
Conclusions
The fusion of network and geographic metrics offers the opportunity to augment network similarity measures as well as fill crucial data gaps about transportation efficiency, accessibility, connectivity, and policies. While most applications of machine learning to transportation networks aim at traffic prediction, flow efficiency, rerouting and robustness, we are particularly interested in public transportation accessibility. Identifying under- and over-serviced areas can help in policy decisions, including infrastructure planning and housing development. Additionally we hope that the fusion of geographic and network measures to score areas by the convenience of, and their reliance on, varying modes of transportation can inform decisions for location services (such as apartment hunting, ride sharing, and new store positioning).
We found that the standard measures of network structure do not provide particularly useful insight into the accessibility characteristics of transportation networks. Although the train, bus, and road networks do exhibit some consistent differences across locations, those structural differences do not translate into differences in the usefulness of the modes of transportation. That is to say, how far one can go in a certain amount of time, how many locations can be reached, and how many people can be serviced are obvious measures of usefulness, but these measures (and the clusters they produce) do not match well with any structural features of those networks. Rather, the speed, variety, and destinations of the links provide the greatest impact. With this in consideration we will reconsider the network measures included in our future analyses and hopefully find novel ways to incorporation them to reveal more useful characteristics.
We also acknowledge the possibility of examining the train, bus, and road networks without the hex grid so that measures from previous analyses could potentially be applied. We could then mix in these single-mode-only measures for region clustering and comparison. Although this is reasonable for the train network if we concentrate on the giant component (that includes a vast majority of stations), the bus and road networks are too fragmentary for their isolated analyses to be robust. And although this would facilitate comparisons with previous research on transportation networks that focus on single modes of transportation, we believe that moving in the direction of being more inclusive of modes of transportation and of geographic data to be more fruitful.
Overall, what we find is that within cities there is a familiar pattern of easily accessible central regions with low populations and regions of higher population density further out, with populations again tapering down even further out. These suburban regions often have convenient public transport to the city centers, but locally require buses and/or cars for transportation in any other direction. We were surprised by the power of the road network for transportation throughout the Tokyo area, including the central area. While buses play a large role in suburban area, their usefulness is largely uniform through most of our area of study.
We find that business hubs, despite having low populations, are so conveniently reachable via train and road systems that they consistently achieve the highest sociability and convenience scores. Suburban regions have more serviceable bus systems, but lower connectivity overall resulting in lower reachable populations despite greater local populations. Despite having the largest and densest public transportation system in the world we find that the road network consistently dominates the train and bus networks for all accessibility measures.
In our analysis of reachability and sociability, we find a high variability in groupings by transportation mode (especially for reachability), implying (as expected) that the transportation networks produce distinct accessibility characteristics. However, we also find that even when the correlation of two variables is high, the clustering methods do not consistently create similar groups from those same variables. Recall the scatterplots of reachability and sociability in Fig. 10. It shows that these two variables, and actually all the core variables, present a rather smooth gradient with occasional lumps of points for cases near borders, with zero values, or without certain modes present. The smoothness of our data helps explain the surprisingly high differences in clusterings. In the absence of clear and distinct clusters of data (and without a known ground truth) it is difficult to evaluate the accuracy of the clustering methods; however, the groups discovered (especially by hierarchical clustering) do pass several intuitive reality checks as well as provide useful information on geographic patterns in several accessibility characteristics.
Because the synergy scores are measures of how additionally accessible a location is by using the modes together, the result that being closer to stations, bus stops, and intersection improves the combinatorical effects of the modes is surprising. Certainly being near a station makes the rail network more useful, but why would it make the bus network more useful too? The reason is that in the train-centric city planning of Japan, most bus routes connect to stations and most expressways run parallel to train tracks. Note the white space in the upper left of each plot in Fig. 13; there are no locations close to a train station and far from a bus stop. However, buses and cars can also travel away from stations in directions that trains can’t go. So while being able to take the bus to the nearest station can enhance the usefulness of that station, on average being near a transportation node of any kind gives you more accessibility for the entire integrated network.
Our analysis of transportation mode dominance revealed several interesting results. For one, driving is dominant everywhere. Naturally buses and cars use the same roads, and cars are faster than buses, so it is not surprising that driving beats buses. For some locations trains can reach further than driving in a given amount of time, but when including the walking time to the station the road system is better on average. Roads also foster a more diffuse spread across the area than rail travel, and this contributes to their superior accessibility. With this in mind we assessed relative dominance: locations where the train or bus network is relatively strong compared to other areas. While this informs us of whether any particular mode has advantages over the others, through this effort we concluded that travel mode convenience is a more useful measure for our practical purposes than dominance.
Our use of clustering to gain additional insight into the transportation mode dominance informed us of the highly localized nature of this characteristic. Some geographic patterns exist where they are strongly correlated with, for example, an absence of train lines. However nearby locations can vary drastically in the relative mode strengths based solely on the distance to the nearest station. So for this characteristic the individual location scores are much more informative than the clusters of such scores.
Future work
Because the dataset is so rich, and there as so many questions it can be used to address, there are naturally many directions planned for future work. By including additional socioeconomic data we will examine the relationship between accessibility and factors such as unemployment, income, home-ownership, household structure, age profile, and crime. We are interested in identifying differences in community structure by transportation mode (Bohlin et al. 2014); that is, which geographic regions are considered to be parts of which neighborhoods when considering different modes of transportation. We obviously wish to pursue questions of robustness and efficiency via knockout and detour analyses. This can address response to accidents/failures, and to identify required structural and throughput changes required to adapt to short-term passenger changes (e.g. the Olympics) and long-term demographic changes (e.g., the aging population, urbanization).
In addition to deepening our analyses, we wish to expand and refine our dataset. For example, we are strongly interested in the impact of bicycle ride-sharing programs on transportation flow (Pucher and Buehler 2012). Although these programs have long been popular in Europe and China, and bicycles usage is high across Japan, there is very little data or analysis on bicycle usage and its interaction with other transportation modes. Although all our networks are abstractions, more realistic assessments of bus transfer and wait times, line-specific train transfer times, practical vehicle speeds, etc. would provide more accurate measures of travel times and distances. The approximations made here suffice for our categorization purposes in this paper, but other purposes may be more sensitive to differences of even a few minutes.
Our multi-faceted scoring of locations by their transportation and demographic features across multimodal transportation has led to insights into which characteristics do and do not form geographic patterns. We found that by clustering the data in different ways we could uncover useful breakdowns of different features, such as cross-mode synergies and relative efficiencies. Our current effort aimed to summarize and visualize the clusters in an intuitive and interactive way that will lead to greater insights and deeper questions. Some of those deeper question involve the role of traditional network analyses techniques in evaluating multimodal transportation networks. Perhaps this research into characterizing and classifying multimodal transportation networks will lead to new metrics that can be applied to other kinds of networks.
The current paper use random locations, and this has pros and cons. We also considered using a Poisson Disk Sampling method (Bridson 2007) to have a more regular and even coverage of the area, but we found that having some points very close together was useful in uncovering the sensitivity of some measures to small differences in location. Going forward we will calculate all the measures on every hex, thus allowing us to discern microvariations in the properties based on location differences as small as 250m across the whole Tokyo Area. Although there is certainly a great deal more work to do towards the goal of understanding accessibility in its many forms, our preliminary exploratory analyses have pointed the way to many fruitful options and opportunities.
Availability of data and materials
As described in the text, the population/mesh data and road network data are openly available from the citations provided. The train and bus network data come from proprietary third-party sources (Ekitan 2019). Additional data and/or plots of data generated (correlation matrices, maps of other experiments, scatter plots of variables, etc.) are available upon request.
Notes
Because we extend the hex creation to within 1 km of the border/coastline, a few selected hexes are slightly outside the relevant region (i.e., over water or in neighboring prefectures) but are still connected via the hex network links.
We also processed normalized data, \((x_{i} - \bar {x}) / std(x)\), but do not include this analysis in the results or discussion because the results are too similar to merit it.
Note that because some variables are consistently anti-correlated with others, inverting these measures would result in a higher correlation of the core measure mean value and the distance to Tokyo.
Abbreviations
- AMI:
-
Adjusted mutual information
References
Association for Promotion of Infrastructure Geospatial Information Distribution (2015)
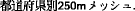 Accessed: 12 Dec 2018. www.geospatial.jp.
Accessed: 12 Dec 2018. www.geospatial.jp.Ayed, H, Galvez-Fernandez C, Habbas Z, Khadraoui D (2011) Solving time-dependent multimodal transport problems using a transfer graph model. Comput Ind Eng 61(2):391–401.
Barthélemy, M (2011) Spatial networks. Phys Rep 499(1-3):1–101.
Berlingerio, M, Koutra D, Eliassi-Rad T, Faloutsos C (2012) Netsimile: A scalable approach to size-independent network similarity. arXiv preprint arXiv:1209.2684.
Bianconi, G (2018) Multilayer Networks: Structure and Function. Oxford University Press.
Biazzo, I, Monechi B, Loreto V (2018) Universal scores for accessibility and inequalities in urban areas. arXiv preprint arXiv:1810.03017.
Bohlin, L, Edler D, Lancichinetti A, Rosvall M (2014) Community detection and visualization of networks with the map equation framework. In: Ding Y, Rousseau R, Wolfram D (eds)Measuring Scholarly Impact: Methods and Practice, 3–34.. Springer, Cham. https://doi.org/10.1007/978-3-319-10377-8_1.
Bridson, R (2007) Fast poisson disk sampling in arbitrary dimensions In: SIGGRAPH Sketches, 22. https://doi.org/10.1145/1278780.1278807.
Calimente, J (2012) Rail integrated communities in tokyo. J Transp Land Use 5(1):19–32.
Clapper, BM (2008) munkres — Munkres implementation for Python. http://software.clapper.org/munkres/index.html.
Crucitti, P, Latora V, Porta S (2006) Centrality in networks of urban streets. Chaos: Interdiscip J Nonlinear Sci 16(1):015113.
Derrible, S (2012) Network centrality of metro systems. PLoS ONE 7(7):40575.
Derrible, S, Kennedy C (2009) Network analysis of world subway systems using updated graph theory. Trans Res Rec 2112(1):17–25.
Derrible, S, Kennedy C (2011) Applications of graph theory and network science to transit network design. Transp Rev 31(4):495–519.
Ekitan (2019) Train and Bus Schedule Data. www.ekitan.co.jp.
GADM (2018) GADM data of Japan 3.6. https://gadm.org/.
Goczyłla, K, Cielatkowski J (1995) Optimal routing in a transportation network. Eur J Oper Res 87(2):214–222.
Guimera, R, Mossa S, Turtschi A, Amaral LN (2005) The worldwide air transportation network: Anomalous centrality, community structure, and cities’ global roles. Proc Natl Acad Sci 102(22):7794–7799.
Hagberg, A, Swart P, S Chult D (2008) Exploring network structure, dynamics, and function using networks. Technical report, Los Alamos National Lab.(LANL), Los Alamos, NM (United States).
Hibino, N, Uchiyama H, Yamashita Y (2005) A study on evaluation of level of railway services in tokyo metropolitan area based on railway network assignment analysis. J East Asia Soc Transp Stud 6:342–355.
Idri, A, Oukarfi M, Boulmakoul A, Zeitouni K, Masri A (2017) A new time-dependent shortest path algorithm for multimodal transportation network. Procedia Comput Sci 109:692–697.
Japan Traffic Safety Association (2017) Rules of the Road. Japan Automobile Federation.
Kivelä, M, Arenas A, Barthelemy M, Gleeson JP, Moreno Y, Porter MA (2014) Multilayer networks. J Complex Netw 2(3):203–271.
Laakso, M, Taagepera R (1979) “effective” number of parties: a measure with application to west europe. Comparative political studies 12(1):3–27.
OECD Statistics (2016) Transport | Transport Measurement | Passenger transport. Accessed: 8 Apr 2019. https://stats.oecd.org.
Official Statistics of Japan (2015)
 /
/ /
/  /
/  /
/ 
 Accessed: 12 Dec 2018. www.e-stat.go.jp.
Accessed: 12 Dec 2018. www.e-stat.go.jp.OpenStreetMap Contributors (2019) Planet dump retrieved from https://planet.osm.org. https://www.openstreetmap.org. Accessed 18 Feb 2019.
Public Purpose (2003) Urban Transport Factbook. Tokyo Yokohama Suburban Rail Summary. http://www.publicpurpose.com/ut-cr-tok.pdf.
Train Media (2017)
 Accessed: 8 Apr 2019. https://www.train-media.net/report/1810/1810.html.
Accessed: 8 Apr 2019. https://www.train-media.net/report/1810/1810.html.Newman, ME (2003) The structure and function of complex networks. SIAM Rev 45(2):167–256.
Pedregosa, F, Varoquaux G, Gramfort A, Michel V, Thirion B, Grisel O, Blondel M, Prettenhofer P, Weiss R, Dubourg V, Vanderplas J, Passos A, Cournapeau D, Brucher M, Perrot M, Duchesnay E (2011) Scikit-learn: Machine learning in Python. J Mach Learn Res 12:2825–2830.
Pržulj, N, Corneil DG, Jurisica I (2004) Modeling interactome: scale-free or geometric?Bioinformatics 20(18):3508–3515.
Pucher, J, Buehler R (2012) Integration of cycling with public transportation:157–181.
Richards, W, Macindoe O (2010) Decomposing social networks In: Social Computing (SocialCom), 2010 IEEE Second International Conference On, 114–119.. IEEE. https://doi.org/10.1109/socialcom.2010.25.
Rodrigue, J-P, Comtois C, Slack B (2016) The Geography of Transport Systems. Routledge.
Soundarajan, S, Eliassi-Rad T, Gallagher B (2014) A guide to selecting a network similarity method In: Proceedings of the 2014 SIAM International Conference on Data Mining, 1037–1045.. SIAM. https://doi.org/10.1137/1.9781611973440.118.
Vinh, NX, Epps J, Bailey J (2010) Information theoretic measures for clusterings comparison: Variants, properties, normalization and correction for chance. J Mach Learn Res 11(Oct):2837–2854.
Acknowledgements
Not Applicable.
Funding
Not Applicable.
Author information
Authors and Affiliations
Contributions
AB and HI conceived of the work; AB designed and wrote the work, as well as performed most of the analyses; MH and ZB helped acquire and analyze data, MH created the map-based visualizations. All authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Competing interests
This research was performed by employees of GA Technologies and may lead to the development of products or information services which may be used by GA Technologies for business operations.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Additional file
Additional file 1
Supplementary materials. Additional data summary tables, plots, and details not required to understand the analyses performed in this work, but perhaps of interest to other transportation network researchers (pdf file). (PDF 6842 kb)
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Bramson, A., Hori, M., Zha, B. et al. Scoring and classifying regions via multimodal transportation networks. Appl Netw Sci 4, 97 (2019). https://doi.org/10.1007/s41109-019-0191-7
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s41109-019-0191-7















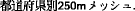 Accessed: 12 Dec 2018.
Accessed: 12 Dec 2018.  /
/ /
/ 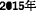 /
/  /
/ 
 Accessed: 12 Dec 2018.
Accessed: 12 Dec 2018.  Accessed: 8 Apr 2019.
Accessed: 8 Apr 2019.